If you want to uncover the most influential, well-connected or important individuals in a network, you should turn to social network analysis centrality measures. These graph analysis algorithms are designed to unpick complex networks and reveal the patterns buried in the connections between nodes. Two of the most powerful are PageRank centrality and EigenCentrality.
In this blog post, we’ll look at how to use these centrality measures in our graph visualization toolkits.
How do they work? When should you use them? Read on to find out.
FREE: Social network analysis & visualization white paper
The ultimate guide to understanding the relationships in any connected dataset
EigenCentrality: understand network influence
EigenCentrality measures a node’s influence. It starts by measuring each nodes ‘degree’ score – which is simply a count of the number of links that node has to other nodes in the network. However, EigenCentrality goes a step further than degree centrality. It goes beyond the first-degree connections to count how many links
Our toolkits calculate each node’s EigenCentrality using the power iteration method. That means our algorithm generates random vectors and multiplies them through an adjacency matrix (a matrix summary of the connections between nodes) until the corresponding eigenvalue is found (or ‘converged’ upon).
What does EigenCentrality tell me?
A high EigenCentrality score indicates a strong influence over other nodes in the network. It is useful because it indicates not just direct influence, but also implies influence over nodes more than one ‘hop’ away.
EigenCentrality in action
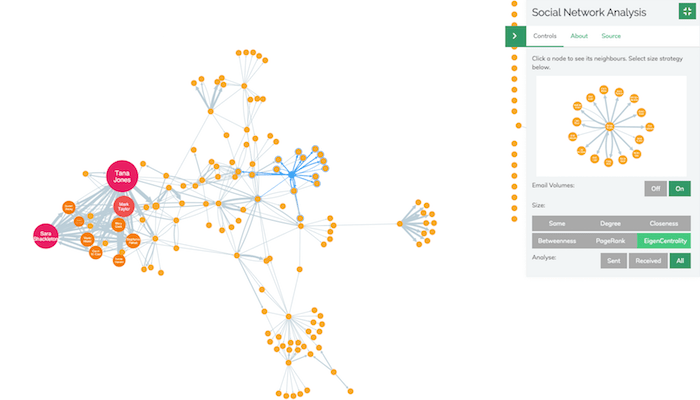
Here’s a good example of EigenCentrality revealing node influence that would otherwise be hidden. In this visualization, we’re looking at around 1.6 million emails sent between Enron employees, published by the Federal Energy Regulation Commission:
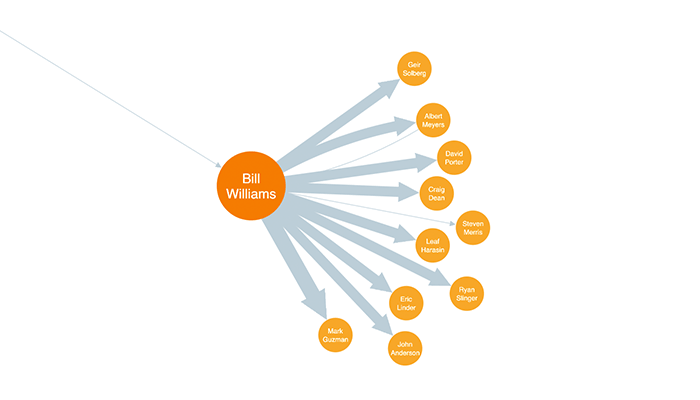
The first image shows nodes sized by degree (i.e. their number of links) which makes Bill look important as he’s sending a lot of emails to his 10-person team.
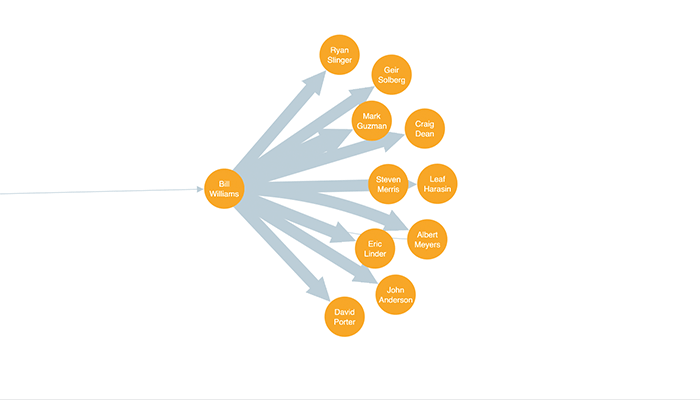
The second image sizes nodes sized by EigenCentrality. This view gives a more complete picture of Bill’s influence. His team is on the periphery of the wider Enron organization, with only one connection back to the wider network – via Timothy Belden, who himself is relatively disconnected from the network’s powerbase:
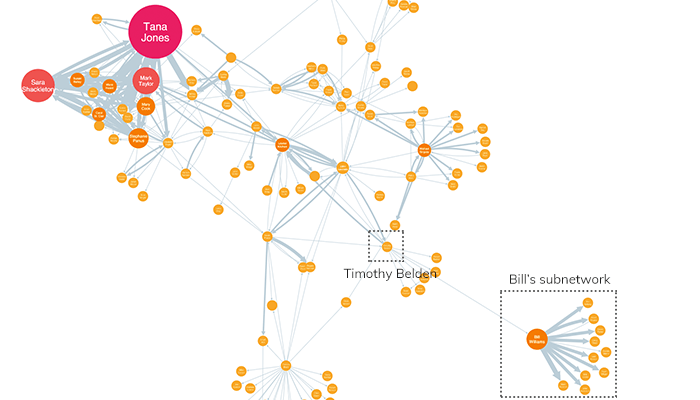
A node may have a high degree score (i.e. many connections) but a relatively low EigenCentrality score, if many of those connections are with other low-scored nodes.
Also, a node may have a high betweenness score (indicating it connects disparate parts of a network) but a low EigenCentrality score if it is distant from the centers of power in the network.
We can see that here with John Lavorato – he’s in the center of the network topologically, but lacks Tana Jones’ volume of connections to high powered nodes:
The ultimate guide to graph visualization
Everything you need to start designing your best graph visualization application.
PageRank centrality: the Google algorithm
Invented by Google founders Larry Page and Sergei Brin, PageRank centrality is a variant of EigenCentrality designed for ranking web content, using hyperlinks between pages as a measure of importance. It can be used for any kind of network, though.
PageRank’s main difference from EigenCentrality is that it accounts for link direction. Each node in a network is assigned a score based on its number of incoming links (its ‘indegree’). These links are also weighted depending on the relative score of its originating node.
The result is that nodes with many incoming links are influential, and nodes to which they are connected share some of that influence.
What does PageRank centrality tell me?
Like EigenCentrality, PageRank can help uncover influential or important nodes whose reach extends beyond just their direct connections. It’s especially useful in scenarios where link direction is important:
- Understanding citations (e.g. patent citations, academic citations)
- Visualizing IT network activity
- Modeling the impact of SEO and link building activity
PageRank centrality in action
Let’s take a look at PageRank in action with the Enron corpus. We’ll follow one employee: Michael Grigsby. With no centrality measures applied, he looks pretty insignificant.
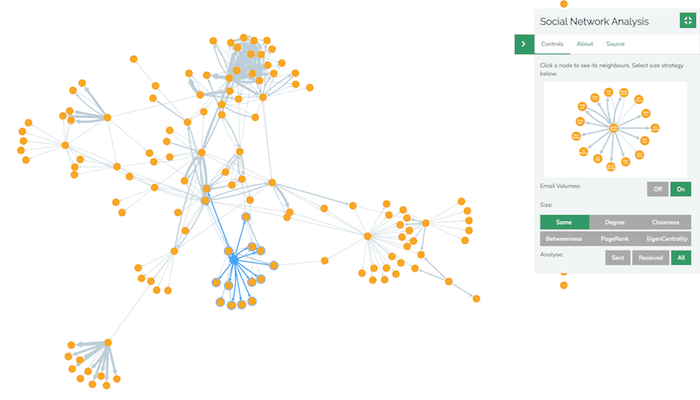
Let’s see how he appears with EigenCentrality applied.
Michael’s low-volume links to other nodes mean he still looks relatively insignificant. Using PageRank centrality, our view is transformed.
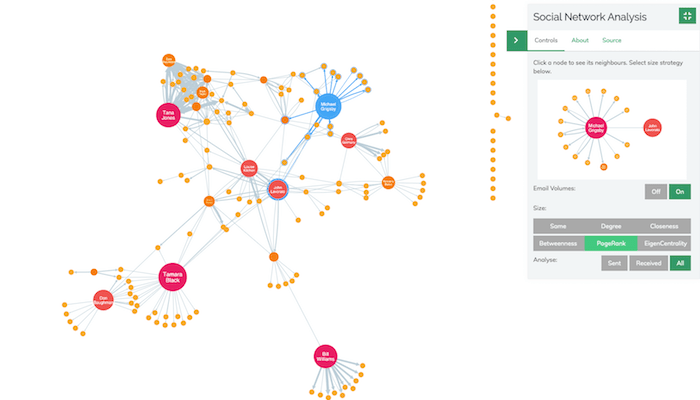
Despite his limited connections, Michael balloons to one of the largest nodes in the network when PageRank is applied. He is one of the few nodes in the network receiving incoming links from highly influential nodes. This has pushed his PageRank score up significantly.
A quick Google confirms that Michael was VP of Natural Gas Trading – an important node in the network that we may not have identified with the other centrality measures.
Find the right centrality measure for the job
Understanding network dynamics and influence can be a game of trial and error. Different measures are better suited to certain scenarios or datasets.
Our toolkits offer a range of social network centrality measures, each designed to uncover different kinds of influence. Download our white paper to learn more.
This post was originally published some time ago. It’s still popular, so we’ve updated it with fresh content to keep it useful and relevant.
