Introducing social network analysis
Social network analysis is a way to understand how networks behave, and uncover the most important nodes within them.
Whether you’re working with social networks, infrastructure and IT networks, or any other kind of complex connected system, these algorithms cut through noisy data to reveal nodes or clusters in the network that require attention.
Let’s take a look at some of the social network analysis measures and algorithms available.
Degree centrality
The degree centrality measure finds nodes with the highest number of links to other nodes in the network.
Nodes with a high degree centrality have the best connections to those around them – they might be influential, or just strategically well-placed.
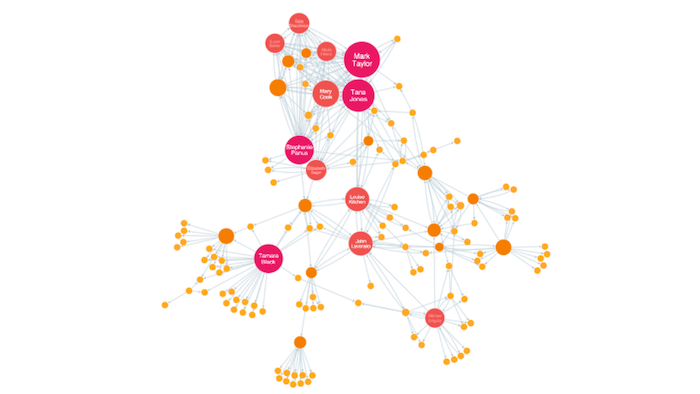
Betweenness centrality
Nodes with a high betweenness centrality score are the ones that most frequently act as ‘bridges’ between other nodes. They form the shortest pathways of communication within the network.
Usually this would indicate important gatekeepers of information between groups.
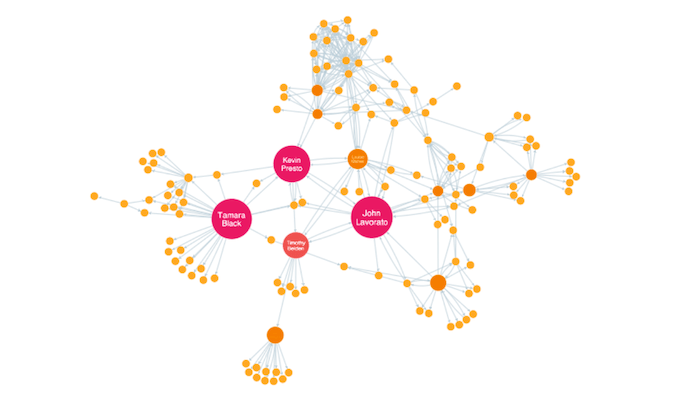
Closeness Centrality
This is the measure that helps you find the nodes that are closest to the other nodes in a network, based on their ability to reach them.
To calculate this, the algorithm finds the shortest path between each node, then assigns each node a score based on the sum of all the paths.
Nodes with a high closeness value have a lower distance to all other nodes. They’d be efficient broadcasters of information.
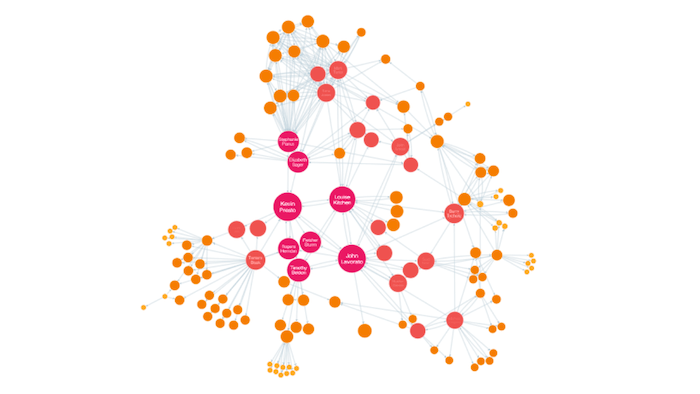
PageRank Centrality
PageRank identifies important nodes by assigning each a score based upon its number of incoming links (its ‘indegree’). These links are weighted depending on the relative score of its originating node.
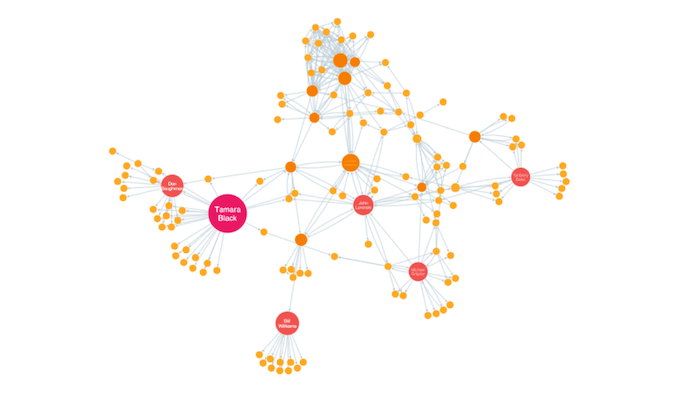
EigenCentrality
Very similar to PageRank, Eigenvector centrality is a measure of influence that takes into account the number of links each node has and the number of links their connections have, and so on throughout the network.
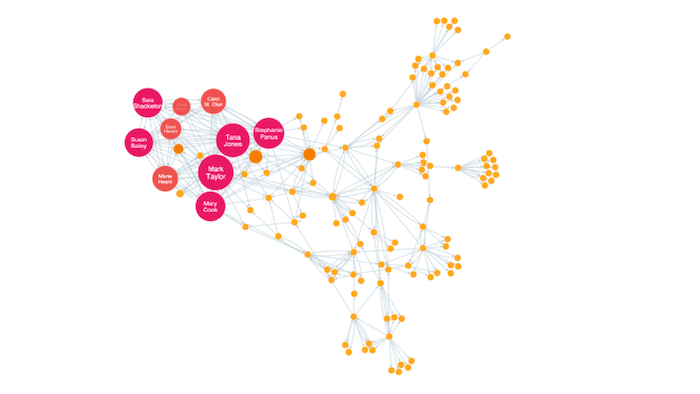
Other Social Network Analysis measures
kCores
This can be a particularly revealing way to drill down into a graph. It works by assigning each node a ‘k’ number, defined by its degree. Nodes are then grouped by their K value and filtered out in turn.
As the low k-value nodes are removed, only clusters of increasingly tight-knit nodes remain. This can help to identify cells or gangs operating semi-autonomously within a wider community.
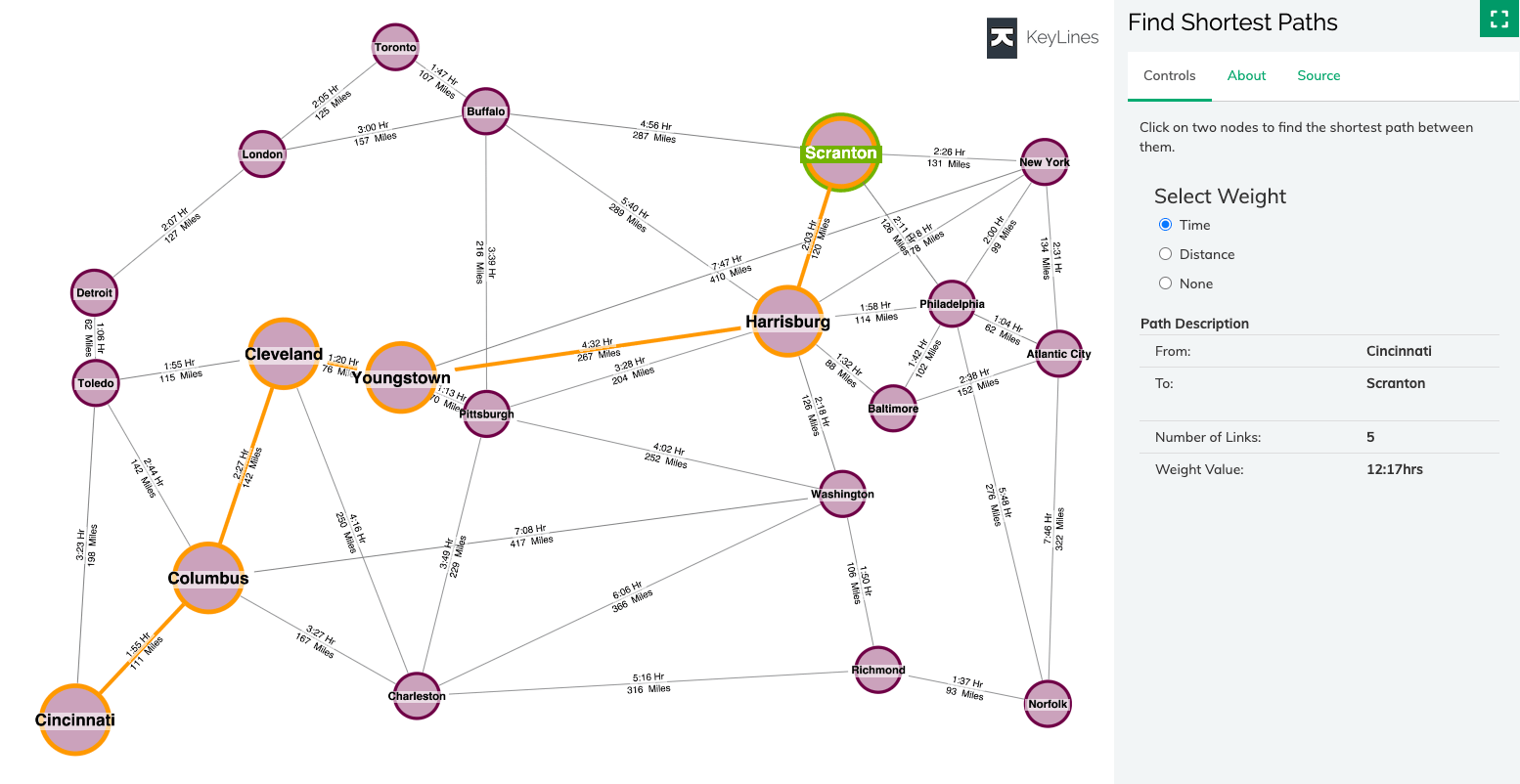
Distance / shortest path
These calculations help your users understand ways to travel through (or ‘traverse’) a network.
The distance function measures how many hops apart two nodes are in a network. Shortest path highlights the route that passes through the lowest number of nodes. Hops can also be weighted, meaning you can calculate actual distances, as well as the number of hops.
White paper: Visualizing social networks
Get a detailed introduction to the topic of social network analysis and visualization.